How Compressionists Think (1) • Jinsung Lee’s Personal Homepage

Source: The Story of Cracking The Enigma Code in 2 Hours

In the early 1940s, as World War II raged across continents, another kind of war unfolded — an invisible one, fought not with bullets but with bits of information.

Both sides sought to intercept, encrypt, and predict each other’s moves through radio transmissions. In the middle of this information war stood Enigma, Germany’s encryption machine — mechanical marvel that turned ordinary text into unreadable cipher. It worked so well that Allied forces, despite intercepting countless German messages, were left staring at random codes.

Desperate for an edge, the Allies assembled a codebreaking team at Bletchley park, led by a brilliant mathematician Alan Turing.

After years of struggle, Turing’s team made a breakthrough: they noticed that many messages sent around 6 a.m. began with the word “Wetterbericht” (German for weather report), and many messages often ended with “Heil Hitler”.

By exploiting these small patterns and repetitions, they dramatically reduced the possible key configurations and finally broke Enigma.

While Turing was decoding messages, there was another young mathematician, Claude Shannon, who was working on the opposite problem: how to make messages impossible to decode. As part of the Allied communications research at Bell Labs, Shannon developed the first mathematical theory of encryption. His classified wartime findings were later expanded to his 1948 paper, “A Mathematical Theory of Communication”.

In it, Shannon established a definition of a “perfect cipher” in a language of math. Specifically, he defined the process of cipher and decipher as the function between message space $M$ and code space $C$ :

M \xrightarrow[\text{(encode)}]{\text{cipher}} C \xrightarrow[\text{(decode)}]{\text{decipher}} M

For arbitrary $m \in M$ and $c \in C$ , Shannon insisted that a theoretically perfect encryption should satisfy:

\mathbb{P}(M=m) = \mathbb{P}(M=m\vert C=c),

which indicates that the probability of predicting the message $m$ should be equal to the probability of predicting it based on the information of $c$ : i.e., the encrypted message $c$ does not contribute to the prediction of the message $m$ , and thus, it indeed well-defines the perfect encryption.

We can also say that the perfect cipher is one where the message and ciphertext are statistically independent—but is such encryption even possible?

Actually, the answer is yes.

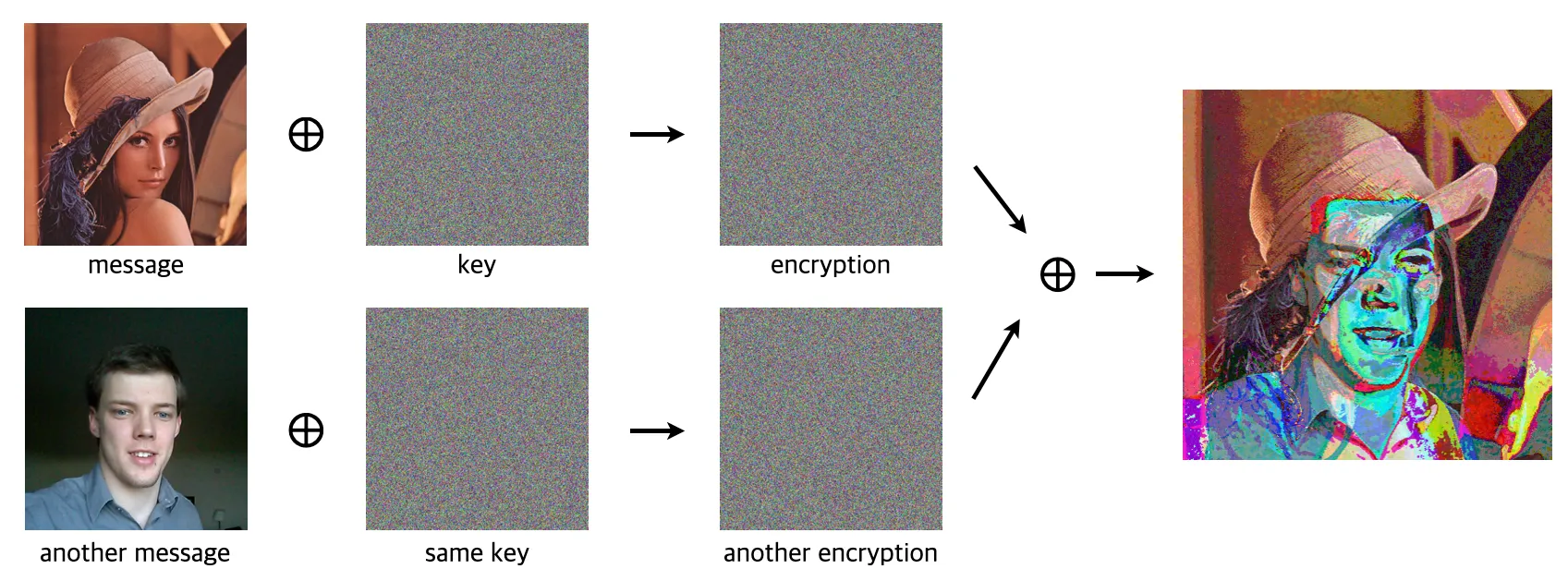
One-time pad example. Source: James Stanley

The one-time pad encryption achieves this ideal by pairing each message with a completely random key of the same length, combining them with an XOR operation. Because the key is truly random and used once, the ciphertext is indeed statistically independent to the original message. However, it is “one-time” for a reason: if the pad is reused, the encrypted message can be easily deciphered by using two encrypted messages that share the same pad.

Since carrying and protecting a unique key for every communication is almost impossible and inefficient, this type of encryption is not adopted in the real world.

In fact, such security and efficiency trade-off leads to an encryption inevitably carrying statistical regularities that the original message has: which means, $\mathbb{P}(M=m) \neq \mathbb{P}(M=m\vert C=c).$

This implies that the understanding of a message can be acquired by finding these statistical regularities—redundancies, repetitions, patterns and structures—in the data, similar to how the encrypted code of Enigma was deciphered.

Here’s where compression comes in to explain its relation to intelligence: being able to compress well means that one is good at finding redundancies and repetitions, which in theory, should be an ultimate skill that is required to understand an unknown thing.

Compressionists

There is a group of people who call themselves “compressionists”, as they believe that studying compression will eventually lead to intelligence.

One of their known activities is “Hutter Prize”: they are giving a grand prize to the person who losslessly compresses the 1GB file of wikipedia into the smallest file size.

The name of the prize was named after Marcus Hutter, who is known for being the author of Universal Intelligence: A Definition of Machine Intelligence (Legg & Hutter, 2007). In this paper, the authors mention “compression test” as a way to measure machine intelligence.

Compression tests. Mahoney has proposed a particularly simple solution to the binary pass or fail problem with the Turing test: Replace the Turing test with a text compression test [Mah99].

Note that all data we perceive and generate are something that is not very friendly to machines: it’ll be like us seeing encrypted codes generated by Enigma. By letting machines to find statistical regularities inside, they might be able to understand human-friendly data just like how Enigma messages were decoded by humans.
And interestingly, this process of “finding regularities” is, at its core, a form of compression.

So, how exactly does compression lead to intelligence?

There are some fascinating examples that show how it works, which we’ll explore in the next sections.

Language models are Compressors

(left) ChatGPT is a Blurry JPEG of the Web was published in The New Yorker. (right) Ted Chiang.

One of my favorite takes on AI comes from Ted Chiang’s 2023 essay, “ChatGPT is a Blurry JPEG of the Web (2023)”.

In it, Ted draws a clever analogy between ChatGPT’s hallucinations and the mistakes made by old Xerox photocopiers.

First column shows the original document, and the rest of the columns show the copied documents by different photocopiers.

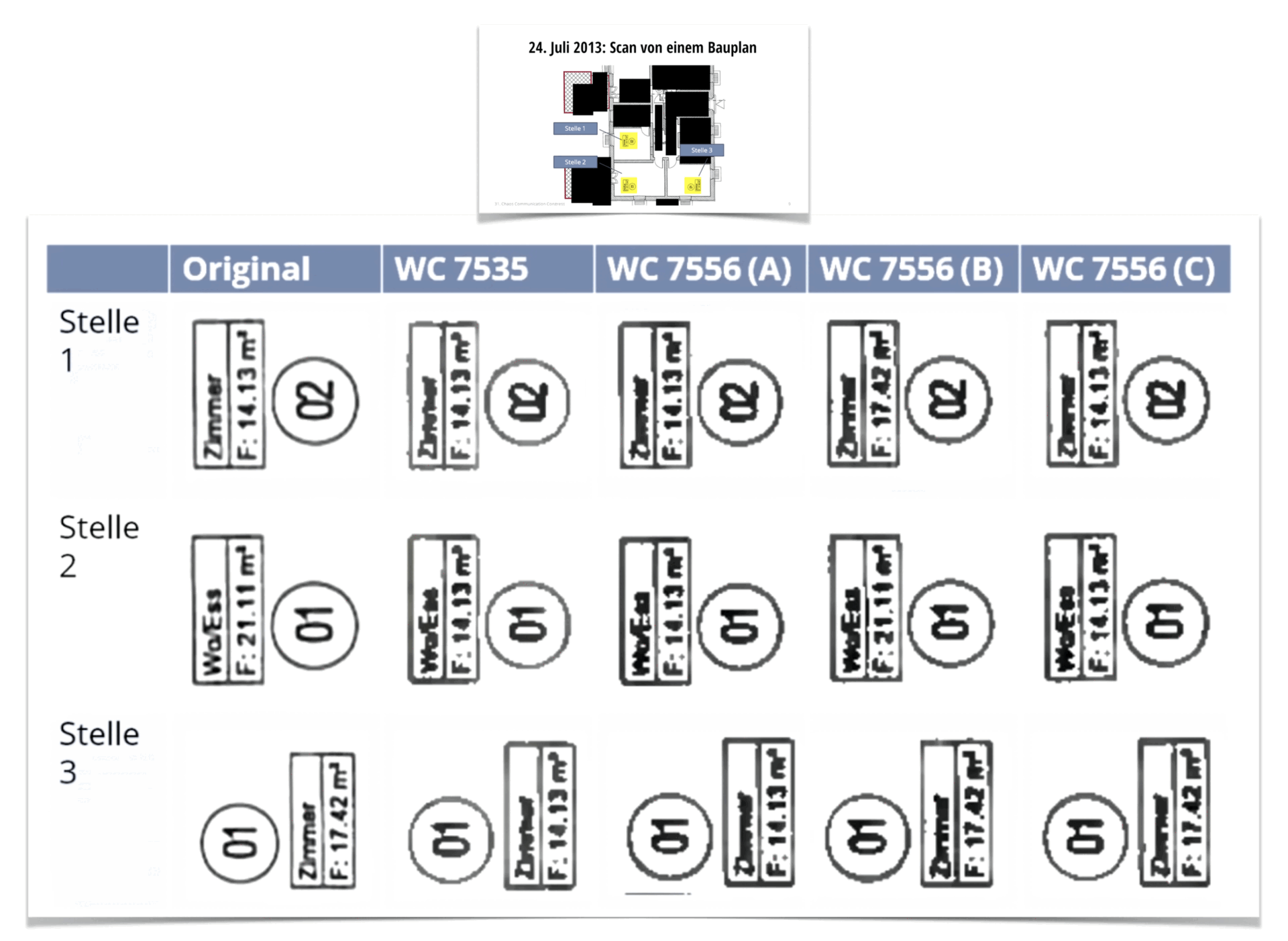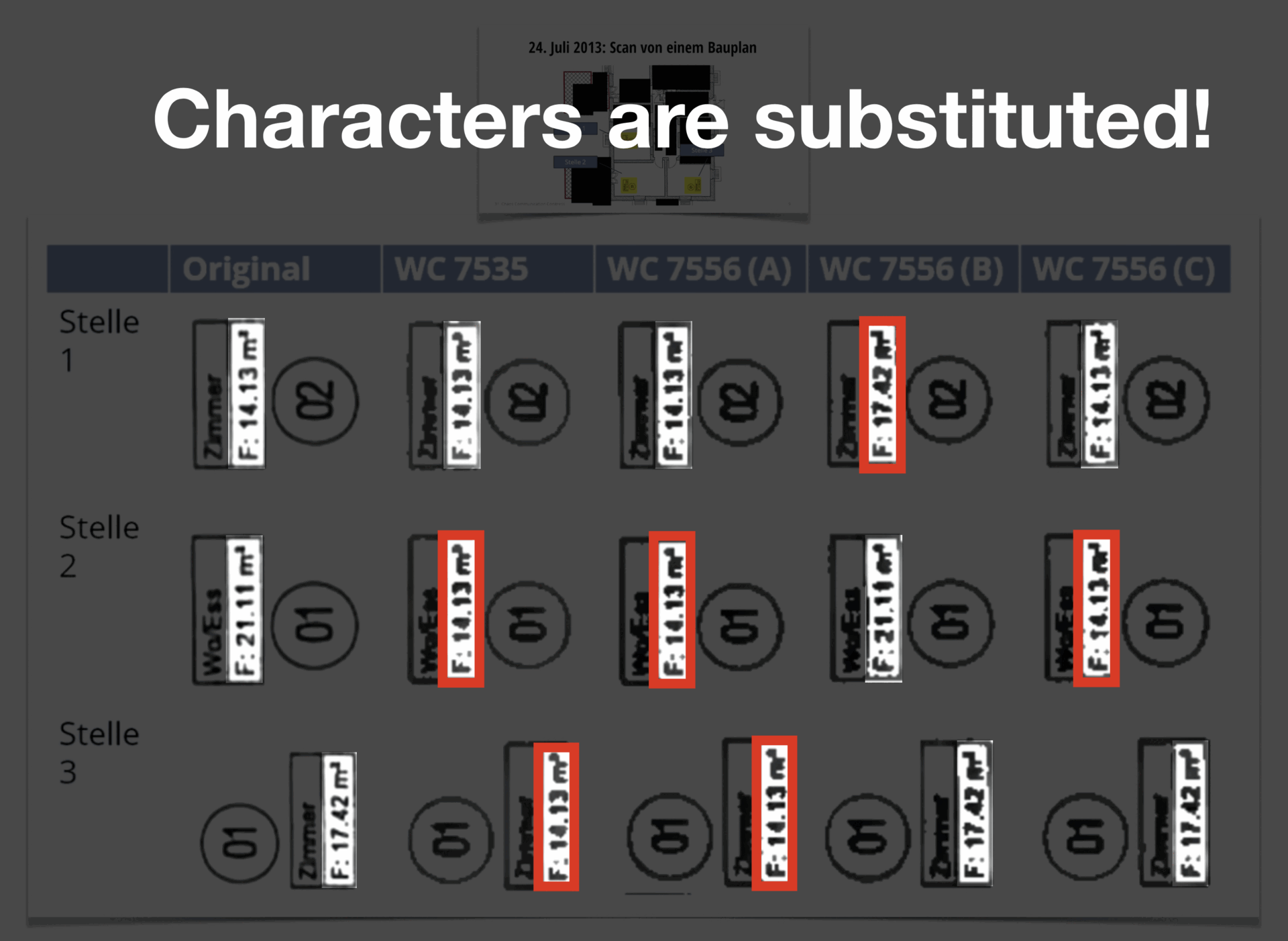
Those machines occasionally swapped letters or numbers in scanned documents — not because they were “broken”, but because of how their compression algorithm worked. To save space, the copier would merge shapes that looked similar, like confusing “8” for a “6”.

Ted further described ChatGPT as a compressed copy of all the entire internet — a single model that squeezes all the text on the Web into a surprisingly compact set of weights. We can “query” this compressed world using natural language, just as if we were searching the Web itself.

But of course, such extreme compression comes at a cost: artifacts. Just like the Xerox photocopiers that sometimes swapped numbers, ChatGPT occasionally hallucinates — generating details that sound plausible but aren’t actually real.

This analogy makes sense in many ways than it first appears. For instance, in image compression, algorithms often use interpolation to fill in missing pixels, and ChatGPT does something similar in “lexical space”: it predicts the most likely words that fit between others, performing a kind of linguistic interpolation.

Interpolation on “image space” vs. interpolation on “lexical space”.

Another example would be “blurriness” defined on both image and lexical spaces. As compression level rises, one cannot accurately recognize the content of an image due to the loss of high-frequency details. We can observe similar phenomena from ChatGPT’s text generation, where the “blurriness” shows up as fuzzy facts or imprecise reasoning.

Blurriness on “image space” vs. blurriness on “lexical space”.

So yes, maybe large language models are just massive compression machines that occasionally pull out the wrong piece of information.

But… what does any of this have to do with intelligence?

Interestingly, a recent paper, Language Modeling is Compression (Delétang et al., ICLR 2024), dives into this question. The authors argue that a language model’s training function is, in fact, a compression objective.

This paper somehow explains how can something as simple as next-token prediction lead to the kind of intelligence we see in language models. For instance, language models are often trained only to guess the next word in a sentence but somehow end up being able to answer questions, reason, and explain concepts, which are not really trivial things we expect from the model to perform.

I find this perspective — seeing language modeling through the lens of compression — very fresh and interesting, and want to share my understanding on this a bit more. Before we dive in, let’s define some math notations to make things clear.

A finite set of symbols $\mathcal{X}$
A stream of data of length $n$
$x_{1:n} := x_1x_2\cdots x_n \in \mathcal{X}^n$
$x_{\leq j} = x_{< j+1} := x_{1:j}$
binary source code (compressor)
$c:\mathcal{X}^* \rightarrow \{0, 1\}^*$

The length of the compressed data using the binary source code $c$
$l_c(x_{1:n})$
A coding distribution
$\rho_n : \mathcal{X}^n \rightarrow (0,1]$ ,
which follows the familiar chain rules:
$\rho(x_{1:n})=\Pi^{n}_{i=1}\rho(x_i|x_{<i})$

We begin with Shannon’s Source Coding Theorem, which tells us that you can’t losslessly compress data to fewer bits than its entropy; i.e., the more regularities the data have, the better it can be compressed.

Using the terms we defined earlier, the theorem is written as:

L \geq H(\rho),

where $L:=\mathbb{E}_{x\sim\rho}[l_c(x)]$ is the expected length of the bitsream $c$ and $H(\rho):=\mathbb{E}_{x\sim\rho}[-\log_2 \rho(x)]$ is the Shannon entropy.

Thus, for better compression, one needs to either hope for the entropy of the coding distribution $H(\rho)$ to be small enough (which we cannot really control), or have the exact information of $\rho$ so that one can achieve the optimal compression.

In practice, we often model a probabilistic model $\hat{\rho}$ to estimate the real target distribution $\rho$ , and instead can achieve a suboptimal code length $\mathbb{E}_{x\sim\rho}[-\log_2 \hat{\rho}(x)] \geq \mathbb{E}_{x\sim\rho}[-\log_2 \ \rho(x)] = H(\rho)$ .

In fact, this suboptimal code length is often termed, cross-entropy loss of the distribution $\hat{\rho}$ realtive to a distribution $\rho$ : $\mathcal{L}(p, \hat{p}) = \mathbb{E}_{x\sim\rho}[-\log_2 \hat{\rho}(x)]$ , which is often used to measure how similar the estimation $\hat{\rho}$ is to the actual distribution $\rho$ . If you look at the term carefully, you’ll see that $\hat{\rho}$ needs to assign higher probabilities to the data likely to be frequently sampled from the target distribution $\rho$ , in order to lower the loss.

This means that the parameterized model $\hat{\rho}$ can learn to resemble the distribution $\rho$ if trained under the cross-entropy loss objective, which in fact, is exactly how language model learns:

\begin{aligned} \mathcal{L}(\rho, \hat{\rho})&:=\mathbb{E}_{x\sim\rho}[-\log_2 \hat{\rho}(x)]\\ &= \mathbb{E}_{x\sim\rho}[-\log _2\hat{\rho}(x_{1:n})]\\ &= \mathbb{E}_{x\sim\rho}\Bigl[\sum^{n}_{i=1}-\log_2 \hat{\rho}(x_{i}|x_{<i})\Bigr]. \qquad (\because \textrm{chain rule})\\ \end{aligned}

Above is often framed as “next-token prediction objective” in the context of machine learning.

Thus, as the model learns to predict the next token more accurately, it simultaneously learns to maximize the achievable level of compression.

Remember that being able to compress well could lead the model to understand things or make it intelligent, one can now roughly see how language models can answer so well to many questions that we ask them just by simply training on next-token prediction task.

Long before the actual language models are invented, Universal Intelligence: A Definition of Machine Intelligence (Legg & Hutter, 2007) already has pointed this out:

To see the connection to the Turing test, consider a compression test based on a very large corpus of dialogue. If a compressor could perform extremely well on such a test, this is mathematically equivalent to being able to determine which sentences are probable at a given point in a dialogue, and which are not.

Additionally, the in-context learning ability of language models is also explainable from this perspective: traditional compressors show higher compression ratio when encountered longer sequences, as they become able to exploit patterns and redundancy in the input sequence. This type of dynamical exploitation could explain the language model being able to better generate answers when given a proper in-context prompt, as the prompts allow them to better understand the data distribution they just have encountered and improve their compress-ability, or, intelligence.

So, if we can measure a machine’s intelligence level by its compress-ability, why don’t we evaluate LLM by making it compress things?

There are several attempts bringing this idea to language model.

LLMZIP: Lossless Text Compression using Large Language Models (Valmeekam et al., arXiv 2023) actually uses LLM to compress English corpora.
Kolmogorov Test: Compression by Code Generation (Yoran et al., ICLR 2025) suggests to evaluate model to create a shortest possible code that is able to generate the dataset (Code golf problem). Note that this code can be interpreted as another form of compression.
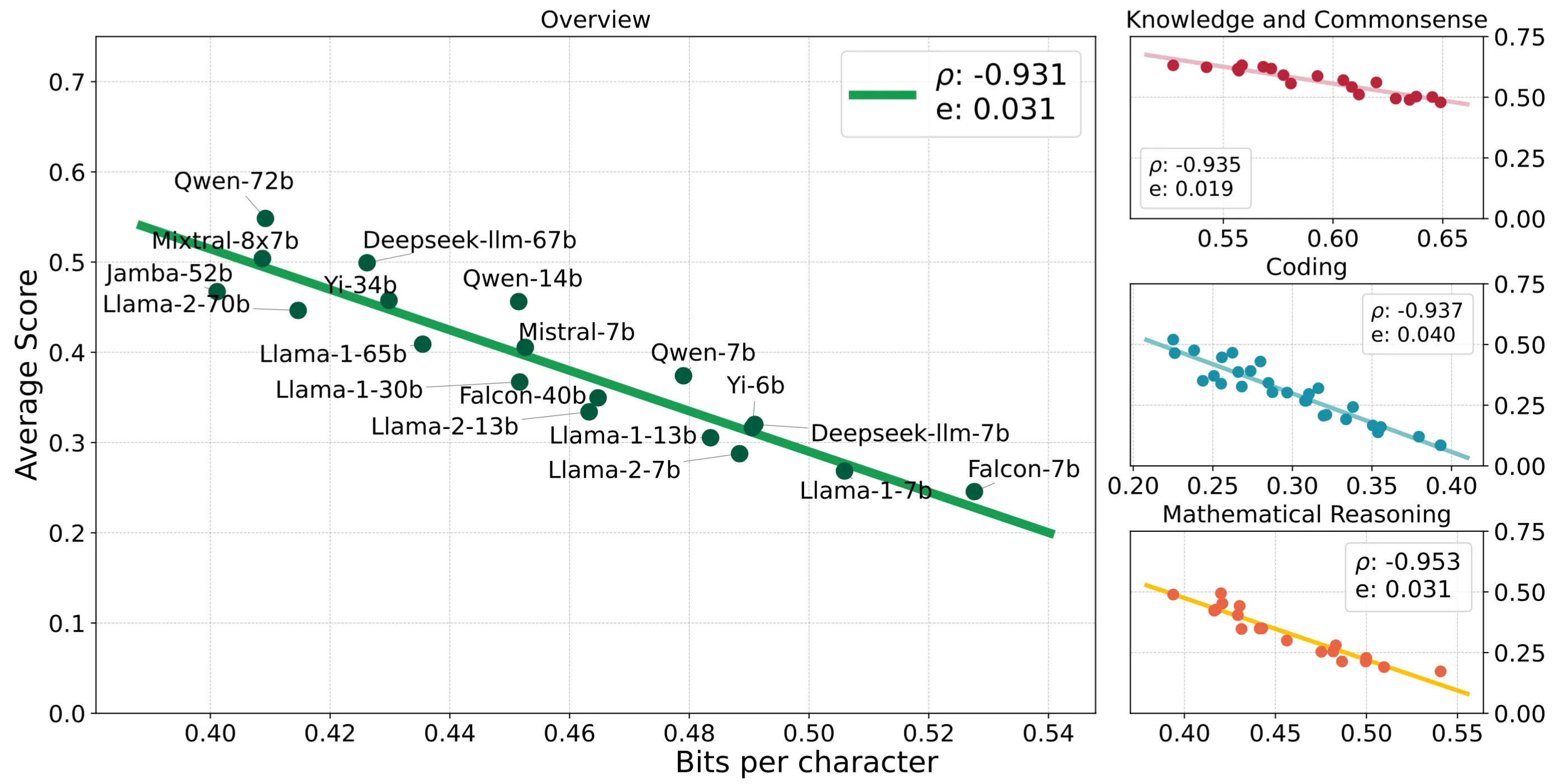
Compression Represents Intelligence Linearly (Huang et al., COLM 2024) shows that the average of the numerous LLM benchmarks is linearly correlated to LLM’s compress-ability.
Figure 1 brought from the paper.

So far, we saw how language models are interpreted as compressors, and observe a close connection between compression and intelligence.

If a compress-ability can function as a quantitative measure for intelligence, would it be possible to train a model to become intelligent just by compressing?

In the next post, I’ll dive into a special case where a model actually develops intelligence purely by training under a compression objective — and interestingly, this one doesn’t even rely on next-token prediction.